背景

常见的排序算法由：插入排序，冒泡排序，shell排序，快速排序，堆排序，归并排序，基数排序等等。
其中，快速排序使用的最为广泛，因为它实现简单、时间复杂度和空间复杂度较低。

一、经典快排

Classic Qucik Sort

1. 描述

1.1 分解divide

将数组A[ p, …, r]划分为两个子数组A[ p, …, q-1]和 A[q+1, …, r], 使得A[ p, …, q-1]中的每个元素都小于等于A[q]，且A[q+1, …, r]中的每个元素都大于A[q]

1.2 求解conquer

通过递归调用快速排序，对子数组A[ p, …, q-1]和 A[q+1, …, r]分别排序。

1.3 合并combine

两个子数组都是有序的，因此直接合并即可

2. 实现

2.1. pivot的选择

上面的q就是pivot，通常的选择方式有：

• 选取中间的元素
• 选取第一个元素
• 选取最后一个元素

2.2 代码的实现

以下代码都是递归实现的，非递归实现可以看文章末尾

 /**
 * pivot选取中间元素，实现quickSort
 * 
 * @param arr = {6,3,4,1,5,8,7}
 * @param l 初始 0
 * @param r 初始 arr.length -1
 */
public static void quickSort(int[] arr,int l,int r){
    int i = l;
    int j = r;
    int piovt = arr[(l+r)/2];

    while (i<=j) {
        while (arr[i] < piovt) {
            i++;
        }
        while (arr[j] > piovt) {
            j--;
        }
        if(i<=j){
            int tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
            i++;
            j--;
        }
    }
    if(l<j){
        quickSort(arr,l,i);
    }
    if(i<r){
        quickSort(arr,i,r);
    }
}

/**
 * pivot选取第一个元素，实现quickSort
 * 
 * @param arr = {6,3,4,1,5,8,7}
 * @param l 初始 0
 * @param r 初始 arr.length -1
 */
public static void quickSort1(int arr[], int l, int r){
    int i;
    int j;
    //递归终止条件
    if(l<r){
        i = l;
        j = r + 1;
        while(true){
            do{
                i++;
            }while(arr[i] < arr[l] && i < r);

            do{
                j--;
            }while(arr[j] > arr[l] && j > l);

            if(i<j){
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }else{
                break;
            }
        }
        //交换哨兵位置
        int temp = arr[j];
        arr[j] = arr[l];
        arr[l] = temp;
        quickSort(arr,l,j-1);
        quickSort(arr,j+1,r);
    }
}

/**
 * pivot最后一个元素，实现quickSort
 * 
 * @param arr = {6,3,4,1,5,8,7}
 * @param l 初始 0
 * @param r 初始 arr.length -1
 */
public static void quickSort2(int a[], int p, int r){
    //递归终止条件
    if(p < r){
        int q = partition(a, p ,r);
        System.out.println(q);
        quickSort2(a, p, q-1);
        quickSort2(a, q+1, r);
    }
}
/**
 * 排序并返回pivot的位置
 *
 * @param arr 待排序数组
 * @param p 数组头下标
 * @param r 数组尾下标
 * @return
 */
public static int partition(int arr[], int p, int r){
    //选择尾为pivot元素
    int x = arr[r];
    int i = p-1;
    for (int j = p; j <= r-1; j++) {
        if(arr[j] <= x){
            i++;
            //交换边界位置
            int temp = arr[j];
            arr[j] = arr[i];
            arr[i] = temp;
        }
    }
    //交换r和pivot的位置
    int temp = arr[r];
    arr[r] = arr[i+1];
    arr[i+1] = temp;
    return i+1;
}

3. 性能分析

3.1 Worst-case of quicksort

• 输入数组已经排好序（正向/反向）
• 在最小/大值附近划分（主元的选择）
• 划分的一个子集为空 1 + （n - 1）+ 0

时间复杂度 T(n) = n^2

3.2 Best-case of quicksort

• 每次都是平均分成两个子序列

时间复杂度： T(n) = 2T(n/2) + O(n) = O(nlogn)

3.3 更多的分法

如果是1:9的分法呢？
T(n) = T(n/10) + T(9n/10) + O(n) = O(nlogn)

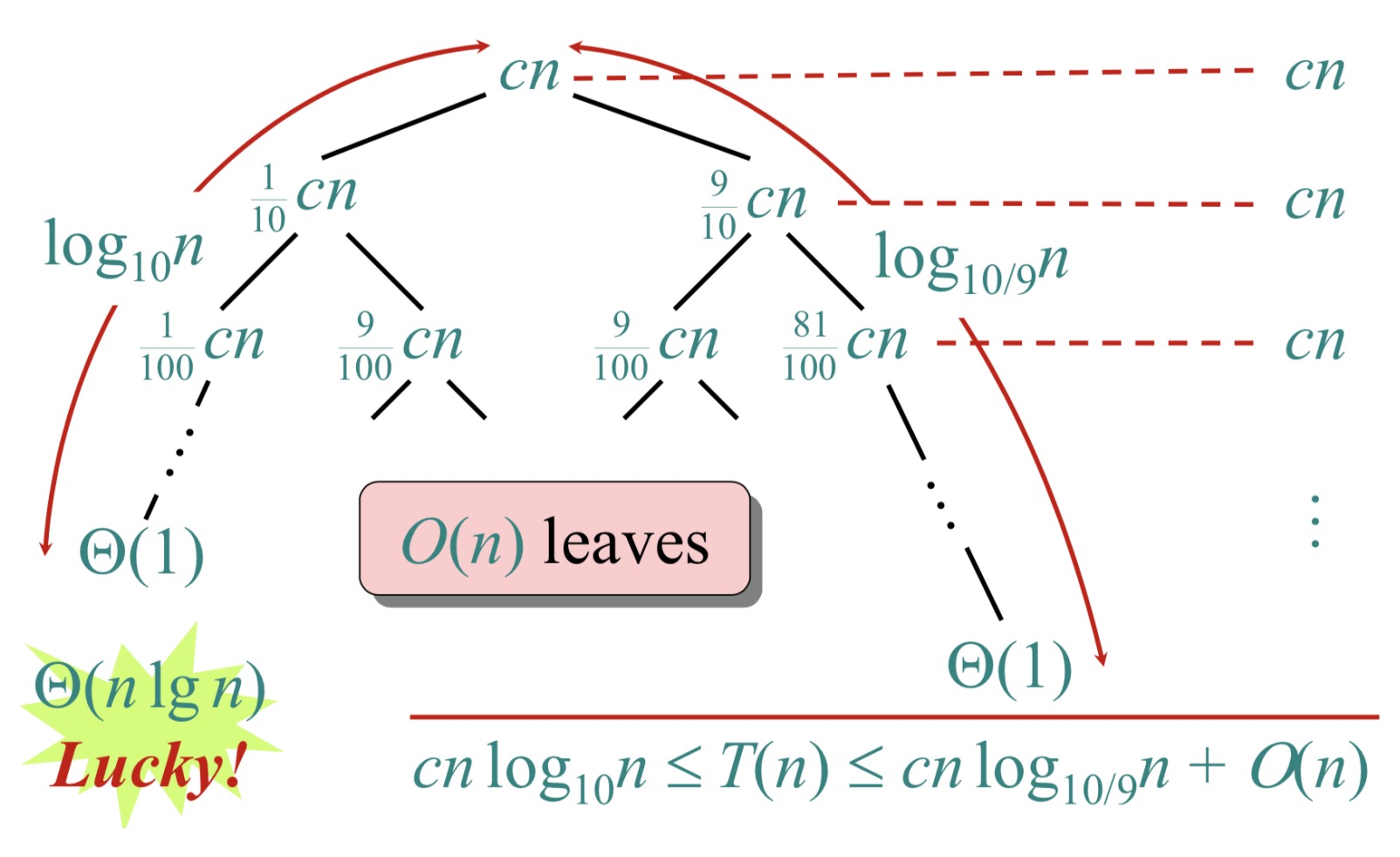
3.4 更有意思的情况

假设每次划分的情况是lucky和unlucky不断交替的，即：
L(n) = 2U(n/2) + O(n)
U(n) = L(n-1) + O(n)

L(n) 
= 2(L((n-1) / 2) + 1/2 O(n)) + O(n)
= 2L((n-1) / 2) + 2O(n)
= 2nlogn
= O(nlogn)

二、随机版本

Randomed-QuickSort
由经典快排，我们可知时间复杂可能为O(n^2), 那为什么快排还能在实际的算法中应用

1. 描述

从子数组A[ p, …, r]中随机选择一个元素作为主元
将随机选择出来的主元与A[r]交换
主元元素x = A[r]是等概率地从 r-p+1 个元素中选出来

2. 实现

/**
 * 随机版本的快排
 * @param arr
 * @param p
 * @param r
 */
public static void quickSortWithRandom(int arr[], int p, int r){
    if(p<r){
        int q = randomPartition(arr, p ,r);
        quickSortWithRandom(arr, p , q-1);
        quickSortWithRandom(arr, q+1, r);
    }
}

public static int randomPartition(int arr[], int p, int r){
    int i = random(p, r);
    //交换i和r的位置
    int temp = arr[r];
    arr[r] = arr[i];
    arr[i] = temp;
    return partition(arr, p ,r);
}

3. 性能分析

• 运行时间不受输入数组顺序的影响
• 不需要对输入的分布做任何假设
• 任何预先设置都不一定会导致最差情况
• lucky / unlucky主要依赖随机数的生产过程

T(n) 是randomized-quicksort的运行时间，因此是一个随机变量。
定义X(k)：将数组分区成（k ：n-k-1）的事件，其中k=0, 1, 2 ... n-1
那么X(k)的取值分为2中情况：

X(k) = 1 能； 
     = 0 否；

假设每次划分都是等概率的，且没有重复元素，那么有

二点分布：
X   1    0
P  1/n   0
则X的期望E(X(k)) = 1 * 1/n + 0 = 1/n

T(n)可以分为以下情况：

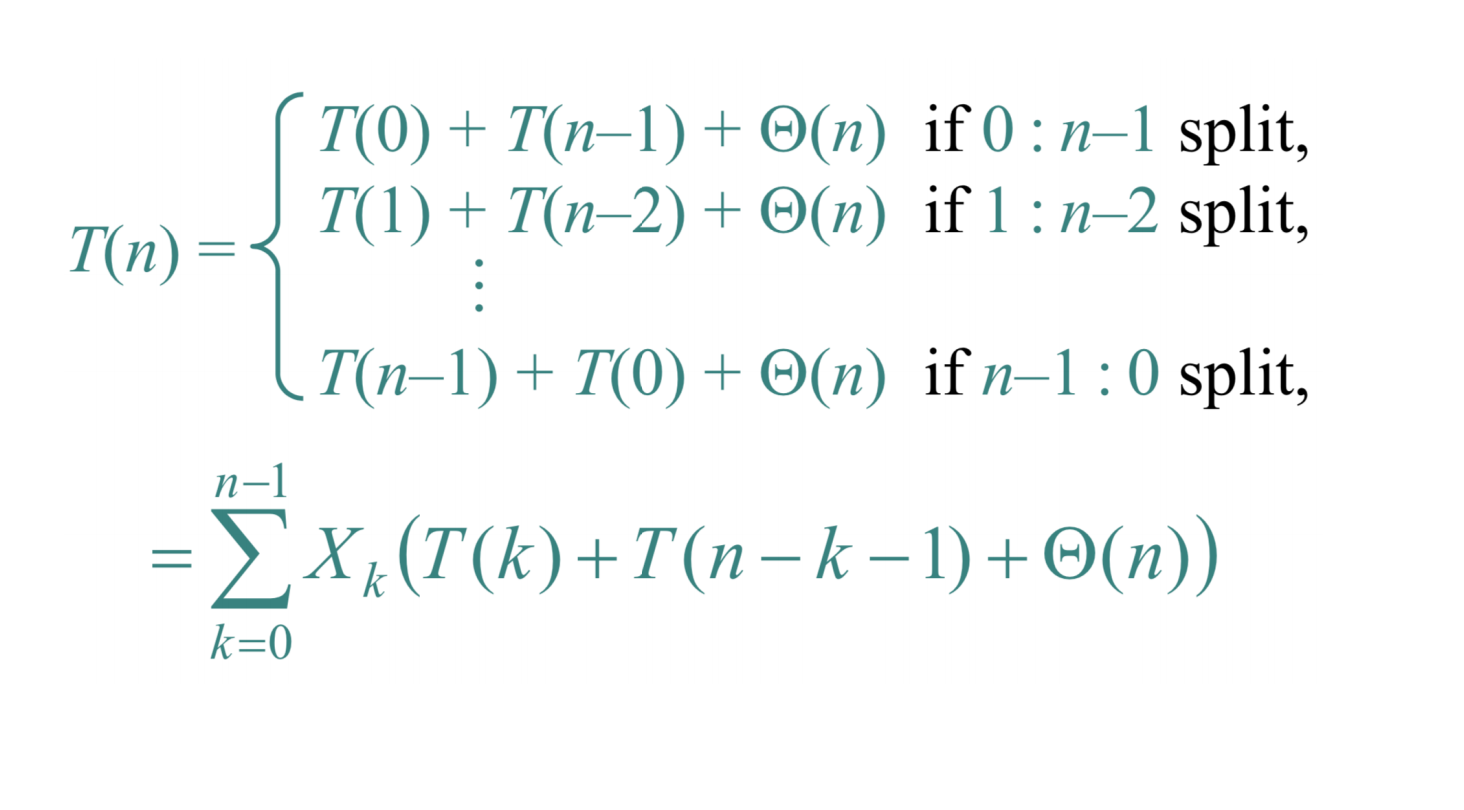
两边求期望：

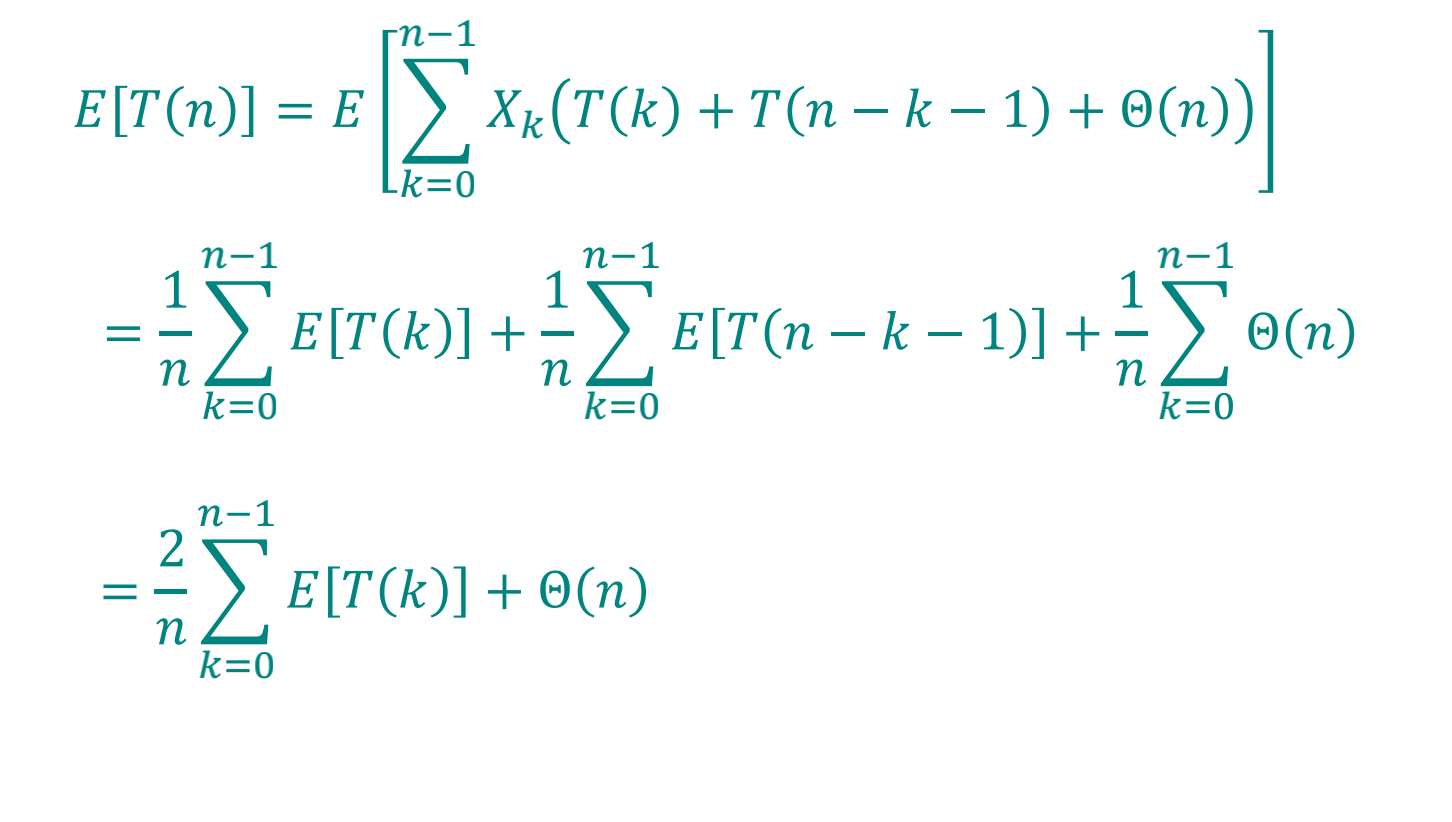
其中：k=0,1两项可以归入O(n)，以下证明E[T(n)] <= anlogn

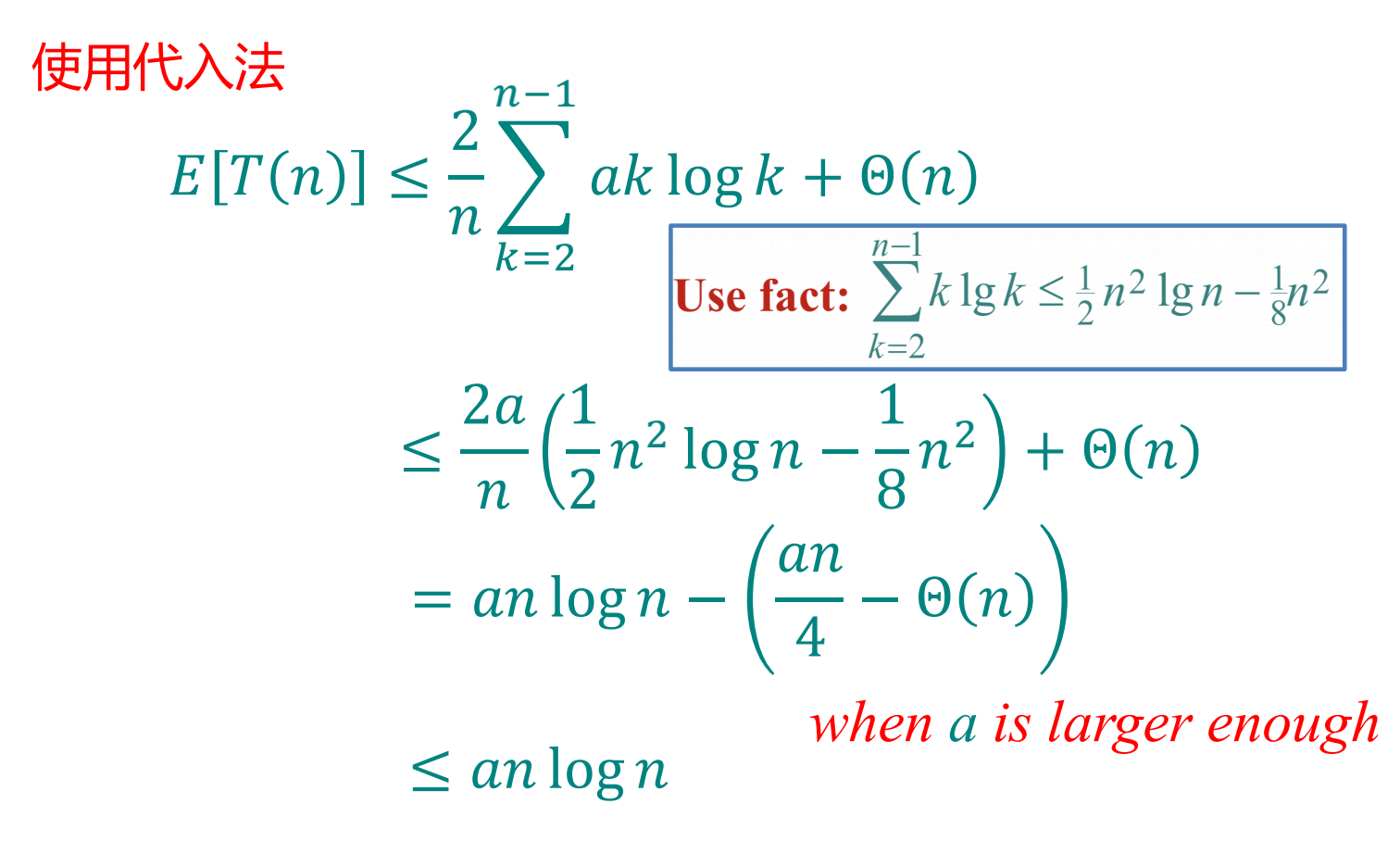
由以上可知
时间复杂度：T(n) = O(nlogn)

附

快速排序的非递归实现，用到了栈

public static void quickSortByStack(int arr[]){
    int length = arr.length;
    int buf[][] = new int[length][2];
    int i,j;
    int pos = -1;
    int l = 0;
    int r = length-1;
    while(true){
        i = l;
        j = r + 1;
        while(true){
            do{
                i++;
            }while(arr[i] < arr[l] && i < r);
            do{
                j--;
            }while(arr[j] > arr[l] && j > l);
            if(i<j){
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }else{
                break;
            }
        }
        //交换哨兵位置
        int temp = arr[j];
        arr[j] = arr[l];
        arr[l] = temp;
        //被分成的前后两部分都不足两个元素
        if(j-1 <= l && j+1 >= r){
            if(pos == -1){
                break;
            }else{
                //获取新的排序范围的起始位置
                l = buf[pos][0];
                //获取新的排序范围的末尾位置
                r = buf[pos][1];
                pos--;
            }
        }else{
            if(j-1>l && j+1< r){
                //分割的部分都超过一个元素
                pos++;
                buf[pos][0] = j+1;
                buf[pos][1] = r;
                r = j-1;
            }else if(j+1>=r){
                //只有前半部分超过一个元素
                r = j-1;
            }else{
                //只有后半部分超过一个元素
                l = j+1;
            }
        }
    }

}

• ← Previous Post
• Next Post →